求阴影部分面积长方形和三角形_求阴影部分面积长方形和三角形

*** 次数：1999998 已用完，请联系开发者***

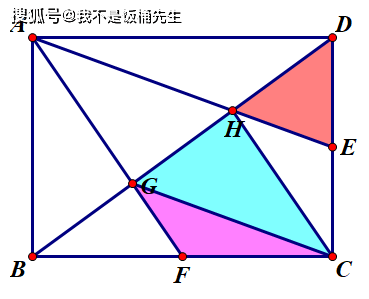
六年级难题:底高未知,求三角形面积,会做的寥寥无几!这是一道小学六年级数学拓展题:难度非常大,会做的寥寥无几!如图, 长方形ABCD面积为96,E在AC上,G在BC上,BG=2CG,DG与AC相交于点F,绿色阴影三角形CDF面积比红色阴影三角形EFG面积多6,求蓝色阴影三角形ABE面积。 提示:等积代换+等高(同底)三角形面积比等于底边(高)之比...

难度超大!长方形面积72,BE=CE,S△BCE=30,求S△ABF?这是一道小学六年级数学拓展题:难度非同一般,班上会做的寥寥无几!如图, 长方形ABCD面积为72,E为长方形内一点,BE=CE,三角形BCE面积为30,AC与BE相交于点F,求绿色阴影部分三角形ABF面积。 提示一:同底三角形面积比等于高之比! ①过点E作BC的垂线EH, 则由BE=CE可知H为...

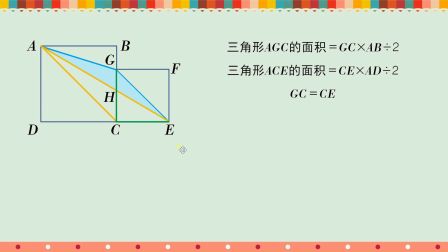
五年级等积代换巧求面积差,会的送分难的大概率交白卷!这是一道小学五年级数学拓展题:会的等同送分,难的大概率要留空白!等积代换、答案跃然纸上!如图, 长方形ABCD面积为10,E为CD右侧任意一点,求蓝色阴影三角形ABE与红色三角形CDF的面积差。 难点:E为CD右侧任意点,故三角形ABE与CDF形状不固定,面积不确定、且无法求出。 ...

难度不小!已知面积求S△DEF这道小学六年级数学题难度不小,有超纲嫌疑!解答过程必须求解一元二次方程!如图, E、F分别在长方形ABCD的边AB和BC上,三角形ADE、BEF与CDF面积分别为60、20和60,EG垂直CD,FH垂直AD,EG与FH相交于点O,求阴影部分三角形DEF面积。 —— 提示: ①连接EH、GH和FG。 ②...

几乎全军覆没,多数孩子空白,学霸口算!难点是确定点B位置解题关键及难点:确定点B位置,即找出暗含条件“B、E、F三点共线”! 如图, 三个相同的长方形,其面积为3,求阴影部分三角形ABC面积。 此题正确率极低的原因在于 ①未告知B点的具体位置; ②示意图未连接BE; ③未告知B、E、F三点关系。 ——— 暗含条件:点B在FE的延长线上,即FE...

一道思考题在班上引起了不小的争议:老师请学霸出场、才得以平息老师在讲完五年级的三角形面积这个单元后,在课堂上出了一道思考题:如图, 长方形ABCD面积为96,E、F分别在AB和BC上,AE=3,CF=4,求阴影部分三角形DEF面积。 这道题难度有点大,会做的孩子寥寥无几,但在班上却引起了不小的争议! 部分同学(称其甲方)这样做: 96=12×8,故结合示...

╯ω╰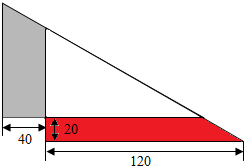

六年级题初中生未必会做!命题老师疏忽,求解需一元二次方程还有部分家长认为,可能是命题老师疏忽了,没有意识到需要使用初中知识!如图, E、F分别在长方形ABCD边AB与BC上,三角形ADE、BEF与CDF面积分别为25、3和32,求蓝色阴影部分三角形DEF面积。 此题的确超纲!即便不超纲,求解难度也非常大! 提示:等高三角形面积比等于底边之比...

五年级口算题,难的大多空白,家长称要用初中知识!补齐长方形、并利用“对角线平分长方形面积”!当然,对大多数孩子来说,此题难度巨大,甚至根本摸不到头脑!如图, ABC为直角三角形,BDEF为正方形,AF=2,CD=8,求阴影部分面积。 此题难在: ①直角三角形AEF与CDE均仅已知一边,无法直接套用三角形面积公式。 ②虽然直角三角形AE...

↓。υ。↓

六年级题目超难几乎全军覆没,初中生做也有难度!绝大部分孩子摸不到头脑、无从下手!如果是填空题或选择题的话,或许还可“投机”使用二级结论“鸟头模型”! 如图, H为长方形ABCD边AD的中点,E、F为BC的三等分点,连接EH和FH、与BD分别相交于点N和M,三角形HMN面积为9,求阴影部分四边形EFMN面积。 提示一:等高(同底)三...