平行四边形有几条底为什么_平行四边形有几条底
*** 次数:1999998 已用完,请联系开发者***

四上数学第五单元第五课:平行四边形知识点与习题一、学习目标解读 1、认识平行四边形,掌握平行四边形的特征,会画平行四边形的高。(重、难点) 2、经历动手操作和自主探究的过程,发展空间观念,提升数学思考能力。 二、详解 1、认识平行四边形 (1)两组对边分别平行的四边形,叫作平行四边形。 (2)从平行四边形一条边上的一点向对...

⊙▂⊙ 四上数学第五单元第五课:平行四边形一、学习目标: 1、重点:理解平行四边形的含义,掌握平行四边形的特征。 2、难点:会画平行四边形的高。 二、详解 1、两组对边分别平行的四边形叫做平行四边形。平行四边形的对边的长度是相等的。 2、平行四边形的特点:平行四边形容易变形,具有不稳定性。
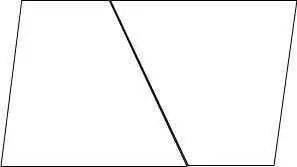
四边形局部面积已知,如何求整体面积?点E、F在平行ABCD边AD上,BF与CE相交于点H,三角形ABE、EFH与CDF面积分别为9、5和6,求平行四边形面积。 ——— 解题关键:利用等积代换、先求三角形BCH面积! —— 提示:等积代换+比例性质(等高三角形面积比等于底边之比)! ①S△BEH+S△BCH=S△BCE=1/2S平行四边形...
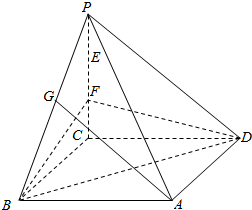
难度不小!S△AEP=8,S△EFP=10,S△DFP=7,求平行四边形面积
●^● 
透视关系让物体有立体感,球体为何是例外?就是画出一个正方形加上两个平行四边形或梯形。很显然,纸上的正方体,除了正对我们的这个面以外,其余的几面都出现了形变,但这种形变并没... 那么物体为什么会存在透视关系呢?简单来讲其实就四个字:近大远小。还是以一条向远方延伸的公路为例,距离我们越近的部分,看起来越大,距...

˙﹏˙ 四上数学第五单元第六课:梯形知识点及习题一、学习目标解读 1、认识梯形,掌握梯形的特征,会画梯形的高。(重点) 2、通过分类、比较、归纳等多种方式,理解平行四边形、梯形、长方形和正方形之间的关系,会用几何图形表示它们的关系。(难点) 3、经历动手操作和自主探究的过程,发展空间观念,提升数学思考能力。 二、详解 1...

四上数学第五单元第六课:梯形知识点与习题全掌握一、学习目标: 1、重点:理解梯形的含义,掌握梯形的特征。 2、难点:会画梯形的高;理解平行四边形和梯形之间的关系。 二、详解 1、只有一组对边平行的四边形叫做梯形。两腰相等的梯形叫做等腰梯形;有一个直角边的梯形叫做直角梯形。梯形有无数条高。 2、长方形和正方形是特殊...
∪﹏∪ 
╯▂╰ 五上数学:任意四边形面积交叉相乘积相等规律揭秘# 交叉相乘积相等及经典例题 ## 一、*交叉相乘积相等* 1. *长方形中的交叉相乘积相等成立* 在长方形的相关几何关系里,交叉相乘积相等这一规律是成立的。 2. *平行四边形中的交叉相乘积相等成立* 同样,在平行四边形当中,交叉相乘积相等这一特性依然成立。 3. *在任意四边形中,交叉...
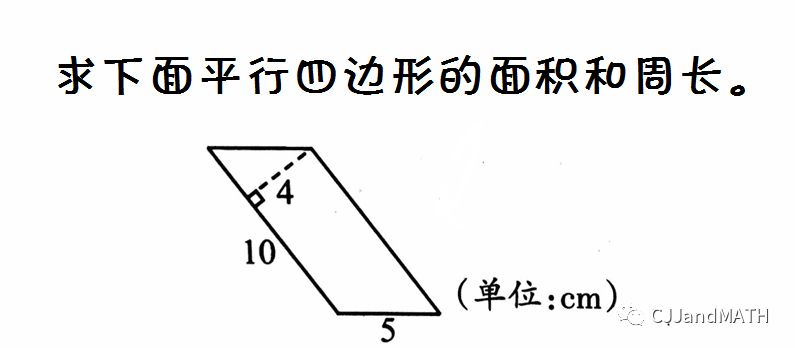
五上数学:任意四边形中面积交叉相乘积相等,交叉相乘积也相等一、交叉相乘积相等 1、长方形中的交叉相乘积相等成立 2、平行四边形中的交叉相乘积相等成立 3、在任意四边形中,交叉相乘积相等成立 4、在梯形中交叉相乘积相等成立 5、研究梯形(蝴蝶翅膀) 二、经典例题 1、一个长方形被分成8个小长方形(每个长方形的长和宽都是整数),其中有...

五上数学:交叉相乘积相等,任意四边形中面积交叉相乘积相等一、交叉相乘积相等 1、长方形中的交叉相乘积相等成立 2、平行四边形中的交叉相乘积相等成立 3、在任意四边形中,交叉相乘积相等成立 4、在梯形中交叉相乘积相等成立 5、研究梯形(蝴蝶翅膀) 二、经典例题 1、一个长方形被分成8个小长方形(每个长方形的长和宽都是整数),其中有...
ˋ﹏ˊ 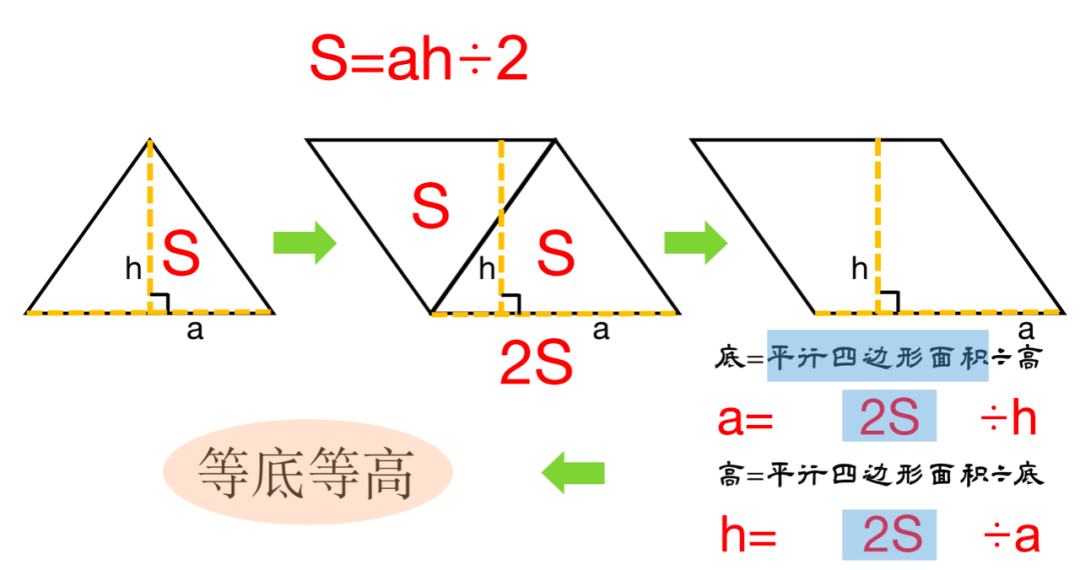
飞飞加速器部分文章、数据、图片来自互联网,一切版权均归源网站或源作者所有。
如果侵犯了你的权益请来信告知删除。邮箱:xxxxxxx@qq.com
上一篇:平行四边形有几条底
下一篇:平行四边形有几条底和高





